Berechnungsverfahren zur Riemannschen Zeta-Funktion

Bei Berechnungsverfahren zur Riemannschen Zeta-Funktion handelt es sich um Algorithmen, die Zahlenwerte ${\displaystyle \zeta (s)}$ für komplexe Werte ${\displaystyle s}$ möglichst genau und zeitschnell ermitteln. Über mehrere Jahrhunderte wurden dabei immer effizientere Verfahren entwickelt. Durch den Einsatz von Computern sind insbesondere seit Beginn des 21. Jahrhunderts sehr umfangreiche Berechnungen möglich.

Die Riemannsche Zetafunktion

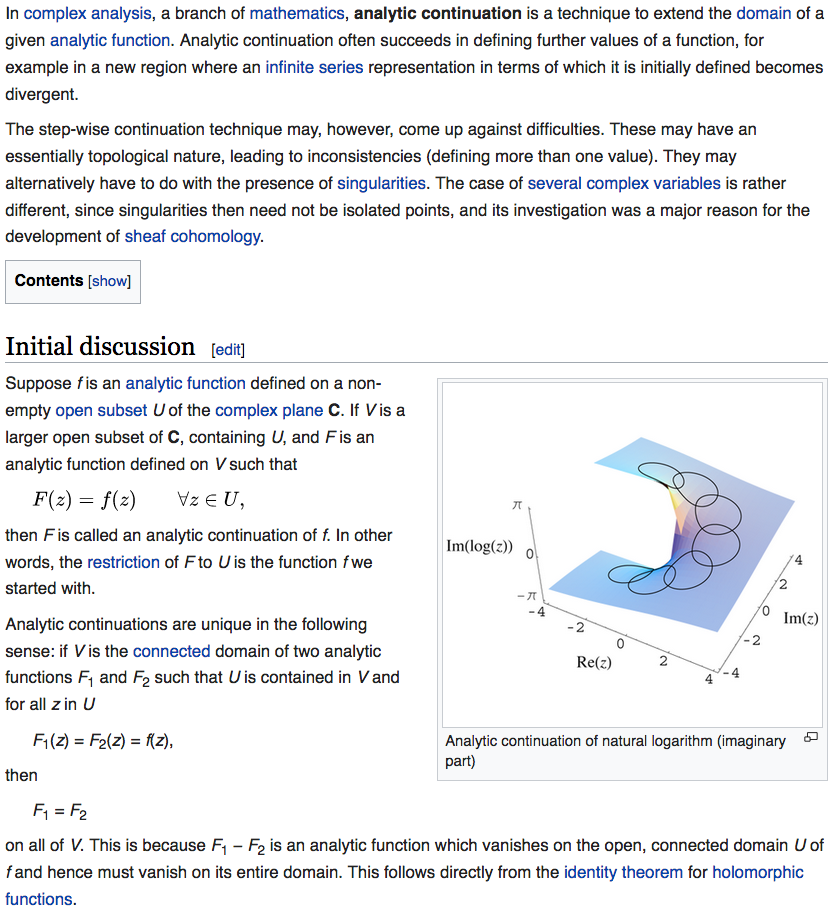
Die Riemannsche Zetafunktion ist eine komplexwertige Funktion, die für eine komplexe Zahl ${\displaystyle s}$ mit einem Realteil ${\displaystyle \operatorname {Re} (s)>1}$ durch die unendliche Summe

${\displaystyle \zeta (s)=\sum _{n=1}^{\infty }{\frac {1}{n^{s}}}=1 {\frac {1}{2^{s}}} {\frac {1}{3^{s}}} {\frac {1}{4^{s}}} \dotsb }$

definiert ist.

Eine der wichtigsten Eigenschaften der Riemannschen Zetafunktion ist ihr Zusammenhang mit den Primzahlen. Sie stellt eine Beziehung zwischen komplexer Analysis und Zahlentheorie her (siehe analytische Zahlentheorie) und bildet den Ausgangspunkt der Riemannschen Vermutung. Der folgende Ausdruck, der auf Leonhard Euler (1748) zurückgeht, stellt den Zusammenhang formelhaft dar als

${\displaystyle \zeta (s)=\sum _{n=1}^{\infty }{\frac {1}{n^{s}}}=\prod _{p\ {\text{prim}}}{\frac {1}{1-{\frac {1}{p^{s}}}}}={\frac {1}{\left(1-{\frac {1}{2^{s}}}\right)\left(1-{\frac {1}{3^{s}}}\right)\left(1-{\frac {1}{5^{s}}}\right)\dotsm }},}$

wobei ${\displaystyle \Pi _{p}}$ ein unendliches Produkt über alle Primzahlen ${\displaystyle p}$ darstellt. Der Ausdruck folgt unmittelbar aus dem Satz über die Eindeutigkeit der Primzahlzerlegung und der Summationsformel für die geometrische Reihe.

Die Funktion lässt sich über den ursprünglichen Konvergenzbereich der Eulerschen Summen- bzw. Produktformel hinaus auf die gesamte komplexe Ebene – mit Ausnahme von ${\displaystyle s=1}$ – eindeutig analytisch fortsetzen. Man erhält eine meromorphe Funktion: Im Punkt ${\displaystyle s=1}$ besitzt sie einen einfachen Pol.

${\displaystyle \zeta (s)={\frac {1}{\Gamma (s)}}\left({\frac {1}{s-1}}-{\frac {1}{2s}} \sum \limits _{n=2}^{\infty }{\frac {B_{n}}{n!}}{\frac {1}{s n-1}} \int \limits _{1}^{\infty }{\frac {x^{s-1}}{e^{x}-1}}\mathrm {d} x\right),}$

wobei ${\displaystyle \Gamma }$ die Gammafunktion und ${\displaystyle B_{n}}$ die Bernoulli-Zahlen sind.

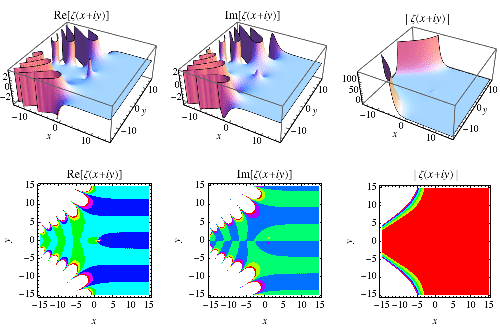
Von großer Wichtigkeit für die Verteilung der Primzahlen ist die genaue Lage der Nullstellen der Zeta-Funktion. Durch numerische Verfahren kann damit in etwa die Riemannsche Vermutung gestützt (jedoch nicht bewiesen) werden.

Geschichte

Die in der zweiten Hälfte des 20. Jahrhunderts aufkommenden leistungsstarken Computer boten neue Möglichkeiten. Bereits im Jahr 1936 hatte der in Oxford wirkende Mathematiker Edward Charles Titchmarsh mit einer Maschine, die ursprünglich für astronomische Berechnungen konstruiert worden war, die ersten 1041 nicht-trivialen Nullstellen der Zeta-Funktion berechnet. Im Jahr 1953 wurden diese Berechnungen von Alan Turing fortgesetzt. Seine Methode wird bis heute benutzt. Erstmals kam dabei ein Computer zum Einsatz. In der Forschung rund um die Riemannsche Zeta-Funktion wurden Computer vor allem nun dazu benutzt, die Korrektheit der Riemannsche Vermutung für möglichst viele Nullstellen zu überprüfen. Obwohl es sich bei allen Rechnungen um numerische Verfahren handelt, zeigen diese exakt und nicht nur annähernd, dass sich die untersuchten Nullstellen auf der kritischen Geraden befinden.

Die Richtigkeit der Riemannschen Vermutung wurde von vielen Mathematikern angezweifelt, unter anderem von Don Zagier. Bei einer Konferenz Anfang der 70er in Bonn spitzte sich eine Diskussion zwischen ihm und Enrico Bombieri schließlich zu und endete in einer Wette: Zagier sagte voraus, es müsse eine Nullstelle der Zeta-Funktion geben, die nicht Riemanns Vorhersage gehorche, Bombieri hielt dagegen. Da beide jedoch nicht davon ausgingen, noch zu Lebzeiten Zeuge eines rigorosen Beweises zu sein, einigten sie sich darauf, dass Zagier verlöre, wenn die ersten 300 Millionen Nullstellen die Vermutung erfüllten. Zu diesem Zeitpunkt waren bereits einige Tausend Nullstellen lokalisiert, doch es gab theoretische Gründe, dass diese auch auf der kritischen Geraden liegen müssten. Wurde die Zahl größer, so wurden diese Gründe schwächer und ab einer gewissen Größenordnung gab es sogar Hinweise, dass die Vermutung falsch sein könnte. Bei den ersten 300 Millionen sei es deswegen laut Zagier „ein Wunder“, falls diese immer noch ausnahmslos auf der kritischen Geraden lägen. Mit der Zeit stieg die Rechenleistung von Computern rasant. Die Größenordnung der Nullstellenzahl aus der Wette geriet damit schon bald in Reichweite. Im Jahr 1979 hatte eine Gruppe aus Amsterdam um Herman te Riele und Richard P. Brent schließlich 200 Millionen Nullstellen überprüft – alle lagen auf der kritischen Geraden. Zagier kommentierte dazu:

Jedoch wusste Hendrik Lenstra, ein guter Freund Zagiers, von dessen Wette und machte te Riele darauf aufmerksam, dass Zagier verlöre, wenn die ersten 300 Millionen Nullstellen auf der kritischen Geraden lägen. Also rechnete die Gruppe bis 300 Millionen und Zagier musste seine Wette einlösen. Mit zwei Flaschen Wein aus Bordeaux ging er zu Bombieri und betonte:

Bis 2005 wurden im Rahmen des sog. ZetaGrid Project durch verteilte Rechner die ersten 10 Billionen Nullstellen überprüft. Alle lagen auf der kritischen Geraden.

Verfahren

Euler-Maclaurin-Summenformel

Als gute und historisch betrachtet früh verwendete Methode erweist sich die „abgebrochene“ Summenformel, die mit Hilfe der Euler-Maclaurin-Summenformel gewonnen wird. Generell wird zunächst eine beliebige natürliche Zahl ${\displaystyle N}$ festgelegt, für die außerdem ${\displaystyle N>|s|}$ gelten sollte. Es gilt dann:

${\displaystyle {\begin{aligned}\zeta (s)=&\sum _{n=1}^{N-1}{\frac {1}{n^{s}}} {\frac {N^{1-s}}{s-1}} {\frac {1}{2}}N^{-s} \sum _{r=1}^{p-1}{\frac {B_{2r}}{(2r)!}}s(s 1)\cdots (s 2r-2)N^{-s-2r 1} R_{2p}(s).\end{aligned}}}$

Dabei gilt für das Restglied

${\displaystyle |R_{2p}(s)|\leq \left|{\frac {s(s 1)\cdots (s 2p-1)B_{2p}N^{-s-2p 1}}{(2p)!(\operatorname {Re} (s) 2p-1)}}\right|.}$

Bei der (freien) Wahl von ${\displaystyle p}$ ist außerdem zu beachten, dass das Restglied nur auf der Halbebene ${\displaystyle \operatorname {Re} (s 2p)>1}$ konvergiert. Daher muss stets ${\displaystyle p>-\operatorname {Re} (s/2)}$ gelten. Für größer werdende Werte von ${\displaystyle N}$ verkleinert sich der Fehler ${\displaystyle R_{2p}}$ demnach rapide.

Durch Anwendung der Funktionalgleichung (eine schnelle Berechnung der Gamma-Funktion und der Exponentialfunktion ${\displaystyle \pi ^{s}}$ ist leicht zu implementieren), kann zudem ohne Einschränkung ${\displaystyle \sigma >0}$ angenommen werden. Hier ist die Summenformel deutlich schneller. Ein Nachteil dieser Methode ist aber, dass sie für wachsende Imaginärteile an Effizienz einbüßt.

Die Nützlichkeit dieser Approximation ist bereits länger bekannt. Beispielsweise ermittelte Leonhard Euler ca. 1734 den Wert von ${\displaystyle \zeta (2)}$ auf etwa 20 Stellen genau, bevor er das Basler Problem, das sich mit dem analytisch „exakten“ Wert von ${\displaystyle \zeta (2)}$ befasste, löste. Diese numerische Auswertung war für ihn die praktische Bestätigung für die Richtigkeit seines exakt ermittelten Wertes.

Weiters fand der dänische Mathematiker Jørgen Pedersen Gram im Jahr 1903 numerische Werte der ersten 15 nicht-trivialen Nullstellen, wobei er die ersten 10 Nullstellen auf sechs und die weiteren 5 auf jeweils eine Stelle nach dem Komma ermittelte.

Beispiele

Als ein Beispiel bietet sich die numerische Annäherung des Zahlenwertes von

${\displaystyle \zeta (2)=1 {\frac {1}{2^{2}}} {\frac {1}{3^{2}}} \dotsb }$

an. Für eine sehr gute Approximation reichen die Werte ${\displaystyle N=5}$ und ${\displaystyle p=2}$ vollkommen aus. Einsetzen ergibt:

${\displaystyle {\begin{aligned}\zeta (2)&=\sum _{n=1}^{4}n^{-2} {\frac {5^{-1}}{2-1}} {\frac {1}{2}}5^{-2} {\frac {B_{2}}{2}}\cdot 2\cdot 5^{-3} {\frac {B_{4}}{24}}\cdot 2\cdot 3\cdot 4\cdot 5^{-5} R_{4}(2)\\&\approx 1^{-2} 2^{-2} 3^{-2} 4^{-2} {\frac {5^{-1}}{2-1}} {\frac {1}{2}}5^{-2} {\frac {B_{2}}{2}}\cdot 2\cdot 5^{-3} {\frac {B_{4}}{24}}\cdot 2\cdot 3\cdot 4\cdot 5^{-5}\\\end{aligned}}}$

Die folgende Tabelle zeigt die numerische Auswertung dieser Rechnung.

Diese mit wenig Aufwand gewonnene Approximation stimmt mit dem tatsächlichen Wert

${\displaystyle \zeta (2)={\frac {\pi ^{2}}{6}}=1{,}644934067\dotsc }$

bereits in sechs Dezimalstellen (gerundet) nach dem Komma überein. Zur Unterstreichung der Effizienz sei bemerkt: Hätte Euler stattdessen einfach nur auch für ${\displaystyle n>4}$ den Wert des Terms ${\displaystyle \textstyle \sum n^{-2}}$ aufsummiert, so wären für die gleiche Approximationsgüte zirka eine Million Summanden nötig gewesen. Geht man davon aus, dass Euler per Hand pro Term durchschnittlich 20 Sekunden Rechenzeit benötigte, hätte dies zirka acht Monate ununterbrochenes Rechnen bedeutet.

Analog kann der Dezimalwert von ${\displaystyle \zeta (1/2)}$ angenähert werden. Hier reicht die Wahl von ${\displaystyle N=4}$ und ${\displaystyle p=2}$.

Auch dieser Wert stimmt auf sechs Dezimalstellen genau.

Alternierende Summen

Ein Verfahren mittels abgebrochener alternierender Reihen stammt von Borwein. Basierend auf konvergenzbeschleunigenden Transformationen angewandt auf die Reihe

${\displaystyle \zeta (s)={\frac {1}{1-2^{1-s}}}\sum _{k=1}^{\infty }{\frac {(-1)^{k-1}}{k^{s}}}}$

erhält man die leicht zu implementierende Formel

${\displaystyle \zeta (s)={\frac {1}{1-2^{1-s}}}\left(\sum _{k=1}^{N}{\frac {(-1)^{k-1}}{k^{s}}} {\frac {1}{2^{N}}}\sum _{k=N 1}^{2N}{\frac {(-1)^{k-1}e_{k-N}}{k^{s}}}\right) E_{N}(s),}$

wobei ${\displaystyle \textstyle e_{k}=\sum _{j=k}^{N}{N \choose j}}$ ebenfalls von der Wahl von ${\displaystyle N}$ abhängt. Diese ist für alle Werte ${\displaystyle \operatorname {Re} (s)>-(N-1)}$ verwendbar. Der Fehler ${\displaystyle E_{N}(s)}$ kann mit ${\displaystyle s=\sigma \mathrm {i} t}$ für ${\displaystyle \sigma >0}$ abgeschätzt werden durch

${\displaystyle |E_{N}(s)|\leq {\frac {1}{8^{N}}}{\frac {(1 |t/\sigma |)\mathrm {e} ^{|t|\pi /2}}{|1-2^{1-s}|}}.}$

Für ${\displaystyle -(N-1)<\sigma <0}$ ergibt sich hingegen

${\displaystyle |E_{N}(s)|\leq {\frac {1}{8^{N}}}{\frac {4^{|\sigma |}}{|1-2^{1-s}||\Gamma (s)|}}.}$

Jedoch gilt auch hier, dass das Verfahren für größer werdende Imaginärteile auf der positiven reellen Seite an Effizienz verliert.

Berechnung auf der kritischen Geraden

Riemann-Siegel-Formel

Viele Methoden verlieren an Präzision, wenn der Imaginärteil des Arguments sehr groß gewählt wird, was bei der Nullstellensuche entlang der kritischen Geraden problematisch ist. Daher greift man hier auf andere Methoden zurück, eine davon ist die Riemann-Siegel-Formel.

Für

${\displaystyle \chi (s)={\frac {(2\pi )^{s}}{2\cos \left({\frac {\pi s}{2}}\right)\Gamma (s)}}}$

folgt mit der Funktionalgleichung der Zeta-Funktion schnell ${\displaystyle \chi (1/2 \mathrm {i} t)\chi (1/2-\mathrm {i} t)=1}$, also ${\displaystyle |\chi (1/2 \mathrm {i} t)|=1}$, d. h., ${\displaystyle \chi (s)}$ bildet entlang der kritischen Geraden nur auf Werte des Einheitskreises ab. Es kann also eine stetige reellwertige Funktion ${\displaystyle \theta (t)}$ implizit durch die Gleichung

${\displaystyle \mathrm {e} ^{\mathrm {i} \theta (t)}=\chi ({\tfrac {1}{2}} \mathrm {i} t)^{-1/2}}$

definieren werden, wobei ${\displaystyle \theta (0)=0}$. Diese wird auch als Riemann-Siegelsche Theta-Funktion bezeichnet. Damit lässt sich schließlich die Riemann-Siegelsche ${\displaystyle Z}$-Funktion definieren:

${\displaystyle Z(t)=\mathrm {e} ^{\mathrm {i} \theta (t)}\zeta ({\tfrac {1}{2}} \mathrm {i} t).}$

Man zeigt leicht ${\displaystyle {\overline {Z(t)}}=Z(t)}$, d. h. ${\displaystyle Z}$ ist sogar eine reellwertige Funktion ${\displaystyle Z\colon \mathbb {R} \to \mathbb {R} }$, wird aber genau dann Null an der Stelle ${\displaystyle t}$, falls ${\displaystyle 1/2 \mathrm {i} t}$ eine nicht-triviale Nullstelle von ${\displaystyle \zeta (s)}$ ist. Es sei ${\displaystyle t>0}$ hinreichend groß gewählt. Für Werte ${\displaystyle m={\bigg \lfloor }{\sqrt {t/2\pi }}{\bigg \rfloor }}$ folgt nun mit der Approximate functional equation

${\displaystyle Z(t)=\mathrm {e} ^{\mathrm {i} \theta (t)}\sum _{n=1}^{m}{\frac {1}{n^{{\frac {1}{2}} \mathrm {i} t}}} \mathrm {e} ^{-\mathrm {i} \theta (t)}\sum _{n=1}^{m}{\frac {1}{n^{{\frac {1}{2}}-\mathrm {i} t}}} O(t^{-{\frac {1}{4}}})=2\sum _{n=1}^{m}{\frac {\cos(\theta (t)-t\log n)}{\sqrt {n}}} O(t^{-{\frac {1}{4}}}).}$

Der Fehlerterm ${\displaystyle O(t^{-{\frac {1}{4}}})}$ kann durch eine asymptotische Entwicklung

${\displaystyle (-1)^{m 1}\left({\frac {t}{2\pi }}\right)^{-{\frac {1}{4}}}\sum _{j=0}^{M}(-1)^{j}\left({\frac {t}{2\pi }}\right)^{-{\frac {j}{2}}}\Phi _{j}(2(t-m)-1) R_{M}(t),\,\,\,\,R_{M}(t)=O(t^{-(2M 3)/4}),}$

beliebig verbessert werden. Exakte obere Grenzen für ${\displaystyle R_{j}}$ ergeben sich für ${\displaystyle t\geq 200}$ über

${\displaystyle |R_{0}(t)|\leq 0{,}127t^{-{\frac {3}{4}}},\,\,\,|R_{1}(t)|\leq 0{,}053t^{-{\frac {5}{4}}},\,\,\,|R_{2}(t)|\leq 0{,}011t^{-{\frac {7}{4}}}.}$

Die explizit bestimmbaren Funktionen ${\displaystyle \Phi _{j}}$ werden mit wachsendem ${\displaystyle j}$ recht kompliziert, die ersten sind gegeben durch

${\displaystyle \Phi _{0}(z)={\frac {\cos({\frac {1}{2}}\pi z^{2} {\frac {3}{8}}\pi )}{\cos(\pi z)}},\,\,\,\Phi _{1}(z)={\frac {1}{12\pi ^{2}}}\Phi _{0}^{(3)}(z),\,\,\,\Phi _{2}(z)={\frac {1}{16\pi ^{2}}}\Phi _{0}^{(2)}(z) {\frac {1}{288\pi ^{4}}}\Phi _{0}^{(6)}(z).}$

Insgesamt ergibt sich für eine ziemlich präzise Berechnung ein Aufwand von ${\displaystyle O(t^{1/2})}$ Rechenoperationen in Form von Termberechnungen mit anschließender Addition. Um Nullstellen zu finden, reicht es schon aus, Bereiche mit Vorzeichenwechsel zu identifizieren (und für deren präzise Bestimmung dann eine Intervallschachtelung durchzuführen).

Ist ${\displaystyle t}$ im Bereich ${\displaystyle 10^{10}}$, so reicht die Wahl ${\displaystyle M=2}$ für eine Präzision mit einem Fehler ${\displaystyle \pm 5\cdot 10^{-20}}$, wobei lediglich ${\displaystyle m\approx 40.000}$ Summanden benötigt werden. Für eine ähnliche Genauigkeit benötigen weniger spezielle Verfahren (wie die alternierende Summe) ca. ${\displaystyle 10^{10}}$ Summanden.

Verfahren von Odlyzko und Schönhage

Im Jahr 1988 entwickelten A. M. Odlyzko und A. Schönhage ein sehr schnelles Verfahren, um Werte der Riemannschen Zeta-Funktion auf der kritischen Geraden zu bestimmen. Dieses basiert auf den Ideen der Riemann-Siegel-Formel, benötigt jedoch nur noch ${\displaystyle O(t^{\varepsilon })}$ anstatt ${\displaystyle O(t^{1/2})}$ Rechenoperationen, wobei ${\displaystyle \varepsilon >0}$ beliebig klein gewählt werden kann. Die Verfeinerung der Rechentechniken basiert auf der schnellen Fouriertransformation.

Fortschritte bei der Berechnung von Nullstellen

Einzelnachweise